Punchlines

• Screw you, I’m not Stupid…. I’m just Chinese.
• Joke’s on you, I’m both Chinese AND stupid.

Setups

• Why is it that toilets have a refractory period?
• The satanic church fights back against the Texas abortion ban.

Completed jokes

• Where did Texas gun control funding go? its illegal to own more than 6 d*l**s there
• Not only did you have to pass normal tests, you had to pass like a thousand COVID tests

DOI: 10.3389/fcomp.2021.642633

One-Liner

Developed a kitchen sink of diagnoses tools and correlated it with biomarkers.

Novelty

The kitchen sink of data collection (phones, tablet, eye tracker, microphone, wristband) and the kitchen sink of noninvasive data imaging, psych, speech assesment, clinical metadata.

Notable Methods

Here’s their kitchen sink

I have no idea why a thermal camera is needed

Key Figs

Here are the features they extracted

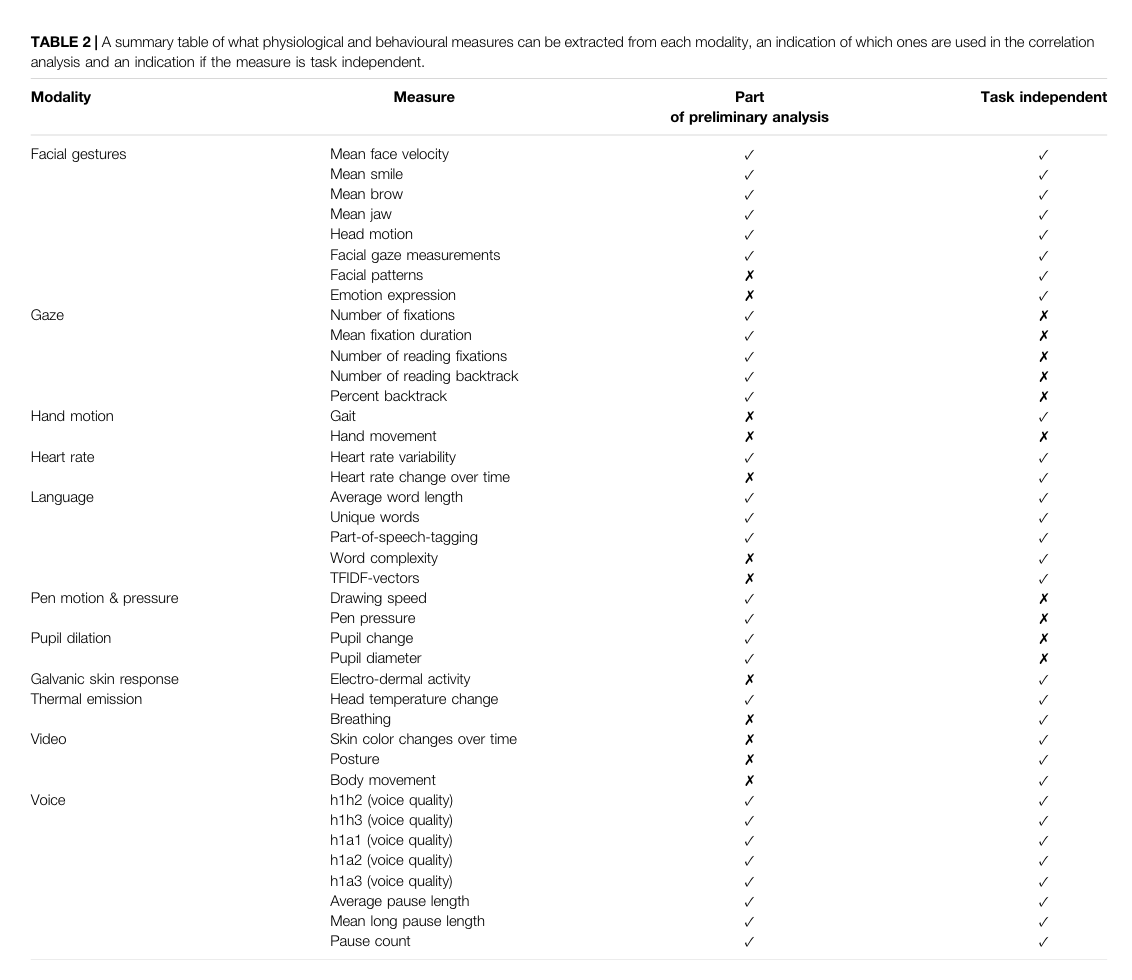
Developed the features collected via a method similar to action research, did two passes and refined/added information after preliminary analysis. Figure above also include info about whether or not the measurement was task specific.

POMDPs can become computationally quite intractable. Alternative: a stochastic, memoryless policy. A policy should be stochastic in order to satisfy certain conditions during adversarial games (think bluffing).

JSJ is basically Q-Learning adapted for POMDPs:

\begin{equation} \begin{cases} Q^{\pi}(s,a) = \sum_{t=1}^{\infty}\mathbb{E}_{\pi} [r_{t}- R^{\pi}|s, a] \\ Q^{\pi}(o,a) = \mathbb{E}_{s}[Q^{\pi}(s,a) | M(s) = o] \end{cases} \end{equation}

where \(M\) is a mapping between states and possible observations.

Policy Improvement

Now, we want to maximise:

\begin{equation} \Delta_{o}(a) = Q(o,a) - V(o) \end{equation}

Ka’chava is described as a “superfood” which is used as a meal replacement to manage hunger.

1. Orbits of planetary bodies are ellipses with the sun at one of the two foci
2. Drawing a line from the sun to the orbiting body, they would sweep out equal areas
3. Planets that are closer to the sun have much shorter periods than that
   • Squares of the periods of the planets is equal to the cubes of the distance from the planet to the sun