identity politics
Last edited: August 8, 2025<> NUS-HIST301 American History
The idea of identity politics is proposed, that politics became associated with sub-population of identities:
- Black Pride Movement
- Chicano Activism
- The American Indian movement
- Termination of reservation system
- Pan-Indian Rights
- Alcatraz and Wounded Knee Occupations
- LGBT movement
- Stonewall
- GLF starts marching
- Asian American
- Yellow Peril
- Model minority movement
- NOW Femanism Acts
- The Equal Rights Act almost possible, and then Phyllis Schlafly happened
- Environmental Movement
- Silent Spring
- Cuyahoga River on fire
- Richard Nixon creates the EPA
- Earth Day
if and only if
Last edited: August 8, 2025to prove that something goes both ways: given \(A\Rightarrow B\), and \(A \Leftarrow B\), \(A \Leftrightarrow B\).
If P != NP, then BPP in P
Last edited: August 8, 2025We really really want to prove:
\begin{equation} \text{BPP} \subseteq \text{P} \end{equation}
which will give \(\text{P} = \text{BPP}\).
How about we replace the truly random bits on the random tape \(r \in \qty {0,1}^{\text{poly}\qty(|x|)}\) with “pseudo-randomness” bits and prove that \(M\) can’t tell the difference.
Namely, a thing that is “pseudo-random” is easier to brute force over. So, we ideally can brute force over \(\text{poly}\qty(n)\) many outcomes instead of \(2^{\text{poly}\qty(n)}\) in the case of true randomness.
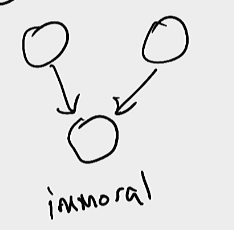
immoral v-structure
Last edited: August 8, 2025v-structure whose parents are unconnected are immoral
This is immoral:
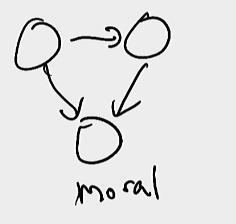
This is moral
Immunogen Design
Last edited: August 8, 2025Using a bunch of signals to create a 3d representation of the system
features
- cyro-EM
- x-ray
- tomo
- glynomics/libidomics
- genetics
studying large-scale viron behavior
Misc. Discoveries bydoing a bunch of MD
- proteins of specific virons “breath”: oning and closing an entire backbone group; this is not yet quantified in physical modeling
- when its open, the “breathing open” motion causes the virus to be vunerable
- *we don’t *
- “we are so biased by what we can see experimentally”
