We have:

\begin{equation} || x ||_{p} = \qty(| x_1 |^{p} + \dots + | x_{n} |^{p})^{\frac{1}{p}} \end{equation}

Real-Time Dynamic Programming

RTDP is a asynchronous value iteration scheme. Each RTDP trial is a result of:

\begin{equation} V(s) = \min_{ia \in A(s)} c(a,s) + \sum_{s’ \in S}^{} P_{a}(s’|s)V(s) \end{equation}

the algorithm halts when the residuals are sufficiently small.

Labeled RTDP

We want to label converged states so we don’t need to keep investigate it:

a state is solved if:

• state has less then \(\epsilon\)
• all reachable states given \(s’\) from this state has residual lower than \(\epsilon\)

Labelled RTDP

We stochastically simulate one step forward, and until a state we haven’t marked as “solved” is met, then we simulate forward and value iterate

Elimination Matricies can be used to derive a LU factorization:

First, this gives an upper triangular matrix

\begin{equation} U = M_{n-1, n-1} \dots M_{22} M_{11} A \end{equation}

We can also create the inverses of each of these:

\begin{equation} A = L_{11} L_{22} \dots L_{n-1,n-1} \cdot M_{n-1,n-1} \dots M_{22} \cdot M_{11} \cdot A \end{equation}

The first half \(L_{j}\) composes a lower triangular matrix; the second half \(M_{j}\) which composes a upper triangular matrix.

LucCage is a platform as a biosensor: a case whose binding domain could be changed to fit specific applications

DOI: 10.1101/2021.03.24.21254263

One-Liner

Review paper presenting the \(ADReSS_o\) challenge and current baselines for three tasks

Notes

Three tasks + state of the art:

• Classification of AD: accuracy \(78.87\%\)
• Prediction of MMSE score: RMSE \(5.28\)
• Prediction of cognitive decline: accuracy \(68.75\%\)

Task 1

AD classification baseline established by decision tree with late fusion

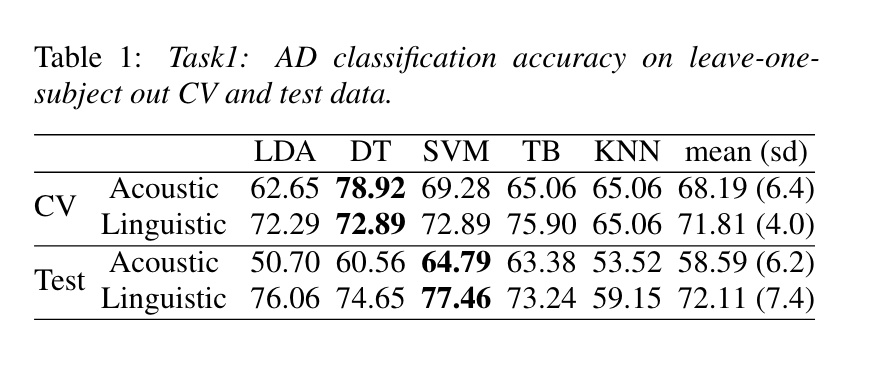
(LOOCV and test)

Task 2

MMSE score prediction baseline established by grid search on parameters.

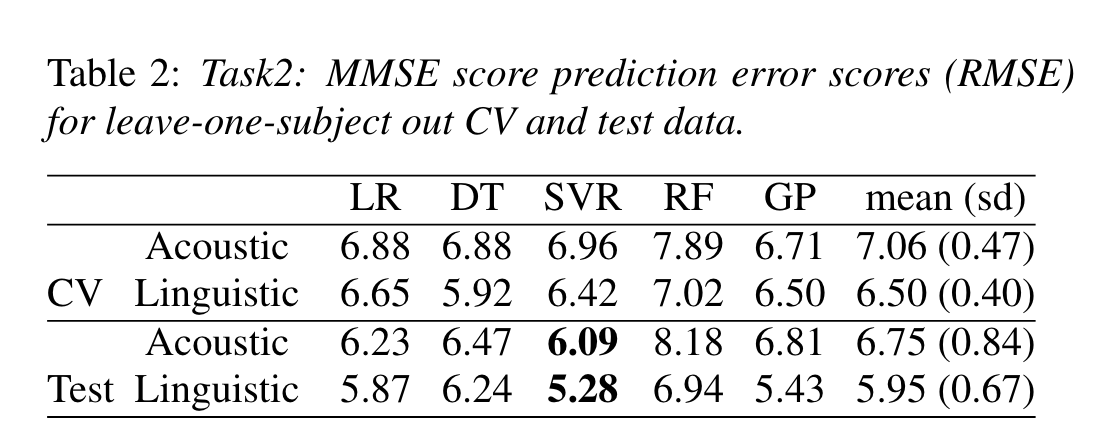
SVR did best on both counts; results from either model are averaged for prediction.