One-Liner

There’s a low-rank “shared” universal subspace across many pretrained LMs, which could be thus leveraged to adapt a model to new tasks easier.

Notable Methods

Did a PCA, and projected variance from one architecture to others (i.e. LoRAs trained for different things).

Define “granularity” as:

\begin{equation} G = \frac{d_{\text{ff}}}{d_{\text{expert}}} \end{equation}

at \(G=1\), we have a dense model; at \(G>1\), we have some kind of MoE.

Here are thy scaling laws:

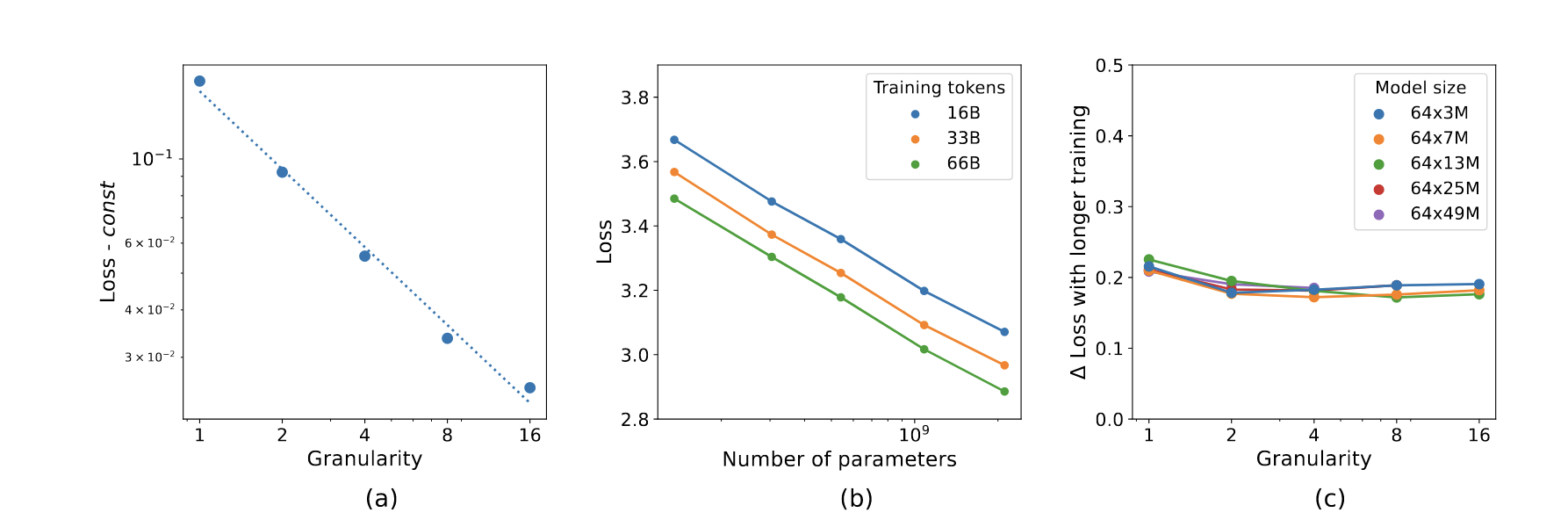
notice how its mostly linear! tiny experts yay!

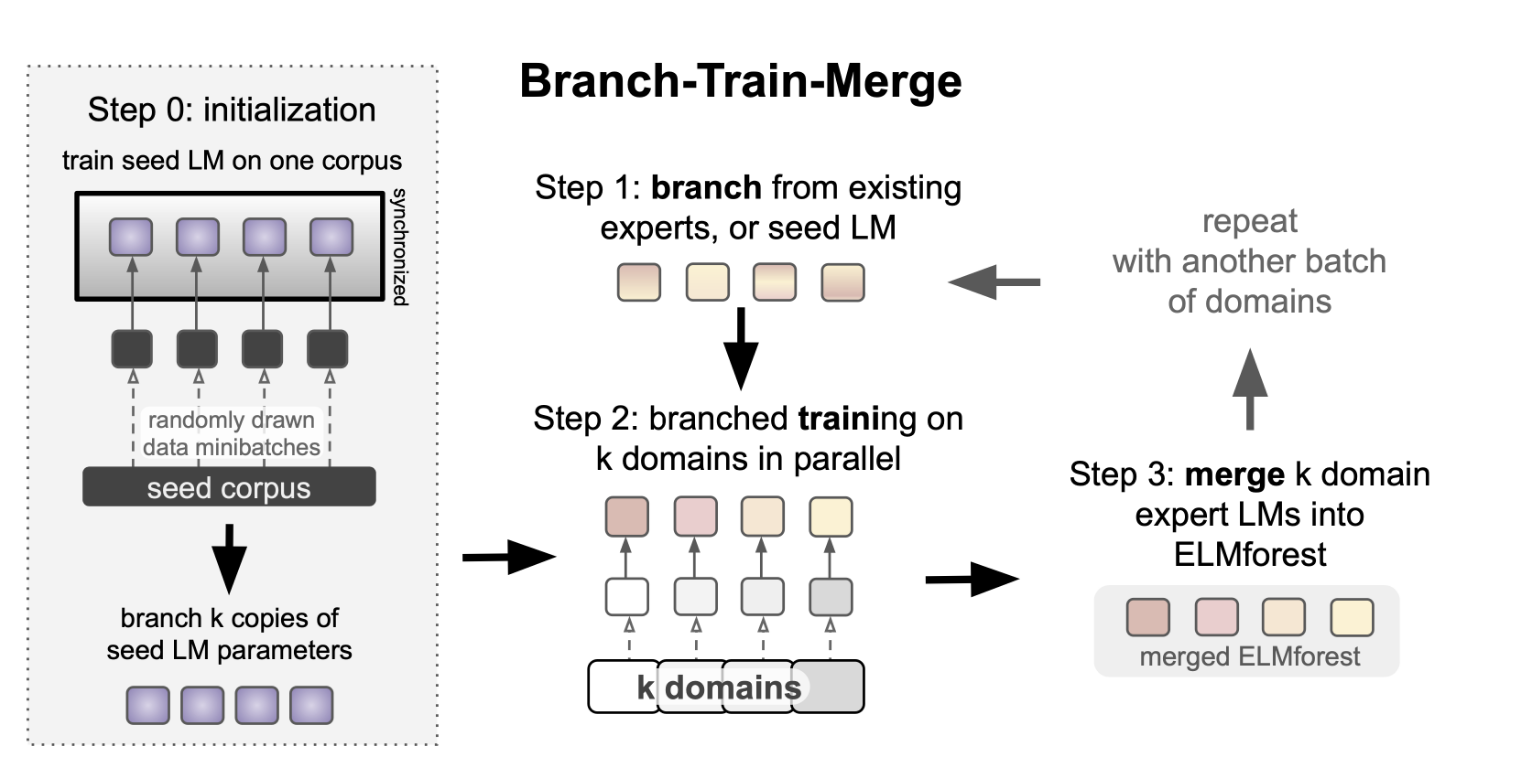
1. weighted parameter average of the existing experts (or copy the new perts)
2. training each expert independently

And then when inference we can use domain-conditioned averaging between the experts by computing:

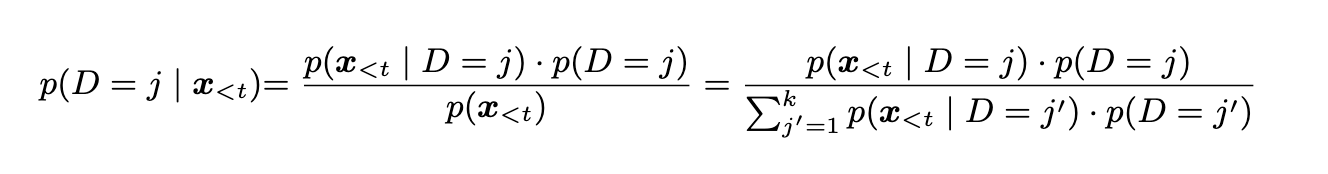
or by averaging the parameters of the experts.

Train experts densely, and then during inference keep only topk

Proposes: more MoEs at later layers + a shared expert.