MaxQ
Last edited: August 8, 2025Two Abstractions
- “temporal abstractions”: making decisions without consideration / abstracting away time (MDP)
- “state abstractions”: making decisions about groups of states at once
Graph
MaxQ formulates a policy as a graph, which formulates a set of \(n\) policies
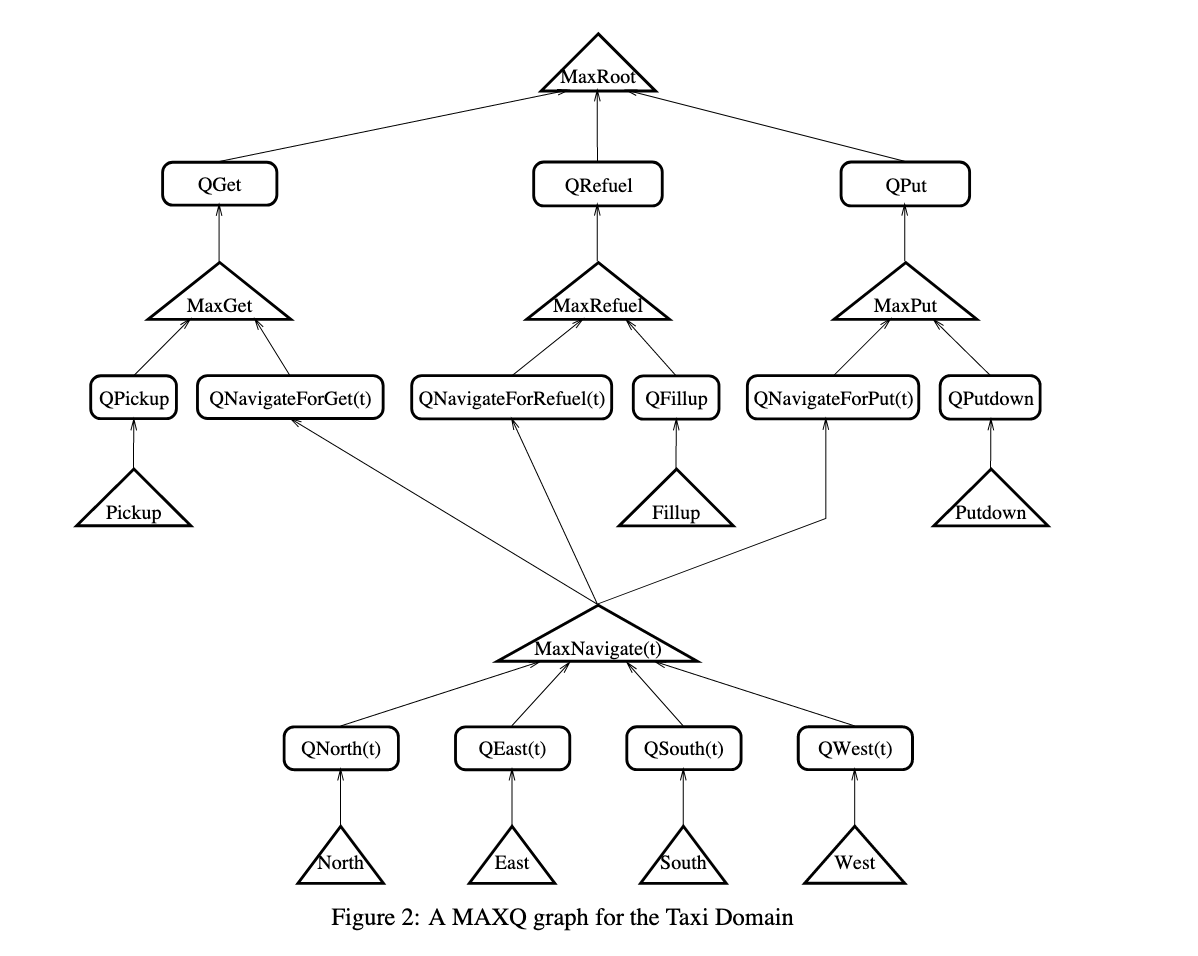
Max Node
This is a “policy node”, connected to a series of \(Q\) nodes from which it takes the max and propegate down. If we are at a leaf max-node, the actual action is taken and control is passed back t to the top of the graph
MBP
Last edited: August 8, 2025MCVI
Last edited: August 8, 2025MCVI solves POMDPs with continuous state space, but with discrete observation and action spaces. It does this by formulating a POMDP as a graph.
Fast algorithms require discretized state spaces, which makes the problem much more difficult to model. MCVI makes continuous representations possible for complex domains.
MC Backup
Normal POMDP Bellman Backup isn’t going to work well with continuous state spaces.
Therefore, we reformulate our value backup as:
\begin{equation} V_{t+1}(b) = \max_{a \in A} \qty(\int_{s} R(s,a)b(s) \dd{s}) + \gamma \sum_{o \in O}^{} p(o|b,a) V_{t}(update(b,a,o)) \end{equation}
meal replacement
Last edited: August 8, 2025mean average precision
Last edited: August 8, 2025- at each point a relevant result is returned, calculate precision
- and then average that
- and then average the precision over all queries
precision
\begin{equation} \frac{tp}{tp + fp} \end{equation}
recall
\begin{equation} \frac{tp}{tp+fn} \end{equation}
accuracy
\begin{equation} \frac{tp + tn}{tp+tn+fp+fn} \end{equation}
f1
\begin{equation} F_1 = \frac{2 (P\cdot R)}{P+R} \end{equation}
