matrix multiplication is defined such that the expression \(\mathcal{M}(ST) = \mathcal{M}(S)\mathcal{M}(T)\) holds:

\begin{equation} (AC)_{j,k} = \sum_{r=1}^{n}A_{j,r}C_{r,k} \end{equation}

While matrix multiplication is distributive and associative, it is NOT!!!!!!!!!!! commutative. I hope you can see that \(ST\neq TS\).

memorization

• its always row-by-column, move down rows first then columns
• multiply element-wise and add (row times column and add)

other ways of thinking about matrix multiplication

• it is “row times column”: \((AC)_{j,k} = A_{j, .} \cdot C_{., k}\)
• it is “matrix times columns”: \((AC)_{. , k} = A C_{., k}\)

matrix as a linear combinator

Suppose \(A\) is an \(m\) by \(n\) matrix; and \(c = \mqty(c_1\\ \vdots\\ c_{0})\) is an \(n\) by \(1\) matrix; then:

a maximal interval is the largest interval you can fit while the function is finite while the function is finite.

maximum a posteriori estimate is a parameter learning scheme that uses Beta Distribution and Baysian inference to get a distribution of the posterior of the parameter, and return the argmax (i.e. the mode) of the MAP.

This differs from MLE because we are considering a distribution of possible parameters:

\begin{equation} p\qty (\theta \mid x_1, \dots, x_{n}) \end{equation}

Calculating a MAP posterior, in general:

\begin{equation} \theta_{MAP} = \arg\max_{\theta} P(\theta|x_1, \dots, x_{n}) = \arg\max_{\theta} \frac{f(x_1, \dots, x_{n} | \theta) g(\theta)}{h(x_1, \dots, x_{n})} \end{equation}

“We find the parameter that maximizes the likelihood.”

1. for each \(X_{j}\), sum
   1. what’s the log-likelihood of one \(X_{i}\)
2. take derivative w.r.t. \(\theta\) and set to \(0\)
3. solve for \(\theta\)

(this maximizes the log-likelihood of the data!)

that is:

\begin{equation} \theta_{MLE} = \arg\max_{\theta} P(x_1, \dots, x_{n}|\theta) = \arg\max_{\theta} \qty(\sum_{i=1}^{n} \log(f(x_{i}|\theta)) ) \end{equation}

If your \(\theta\) is a vector of more than \(1\) thing, take the gradient (i.e. partial derivative against each of your variables) of the thing and solve the place where the gradient is identically \(0\) (each slot is \(0\)). That is, we want:

Two Abstractions

• “temporal abstractions”: making decisions without consideration / abstracting away time (MDP)
• “state abstractions”: making decisions about groups of states at once

Graph

MaxQ formulates a policy as a graph, which formulates a set of \(n\) policies

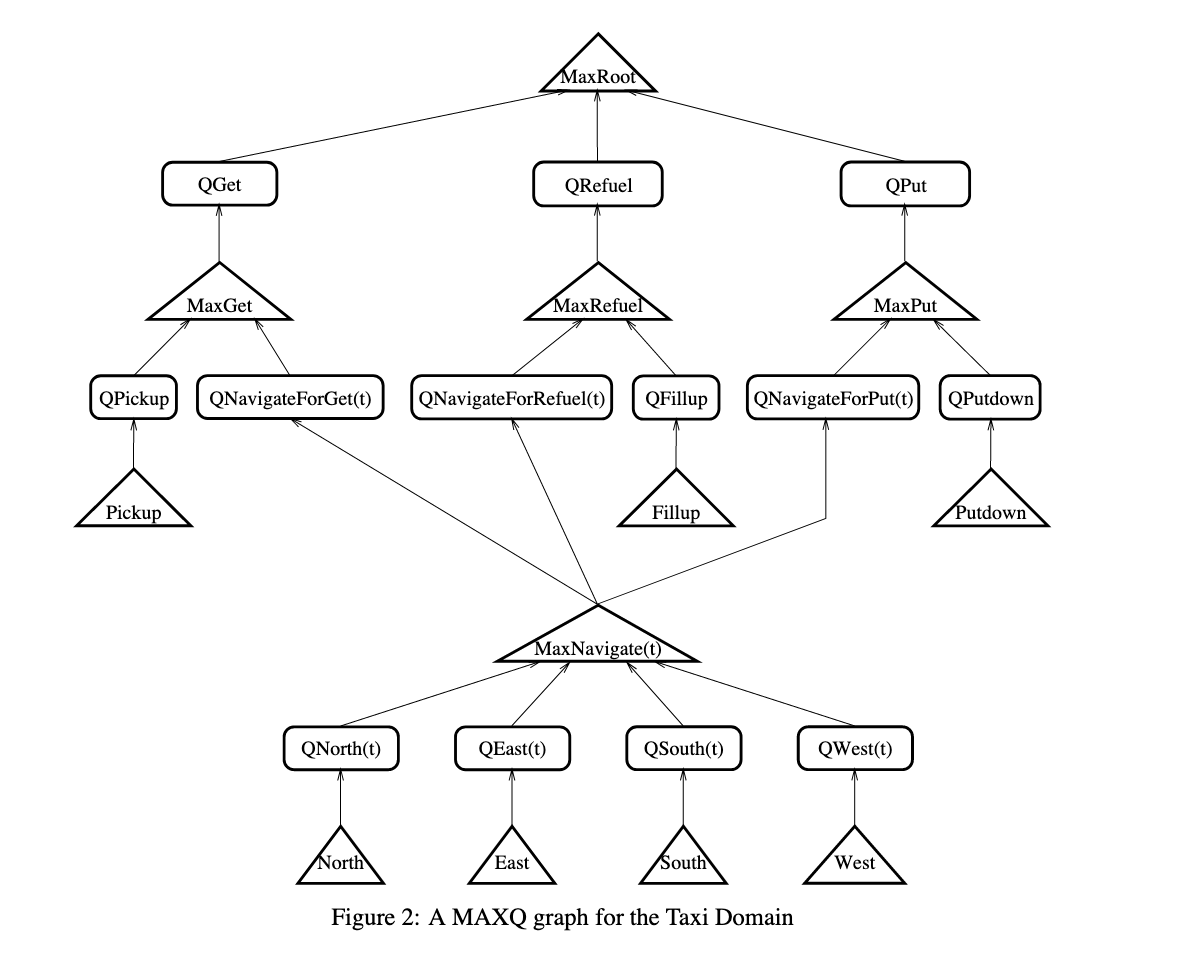
Max Node

This is a “policy node”, connected to a series of \(Q\) nodes from which it takes the max and propegate down. If we are at a leaf max-node, the actual action is taken and control is passed back t to the top of the graph