Non-Linear ODE
Last edited: August 8, 2025Suppose we analyze first order non-linear system:
\begin{equation} x’ = F(t,x) \end{equation}
We can actually turn this into an autonomous system:
\begin{equation} x_0 = t \end{equation}
\begin{equation} x_0’ = 1 \end{equation}
meaning suddenly we have an autonomous system:
\begin{equation} \begin{cases} x_0’ = 1 \\ x_1’ = F(x_0, x_1) \end{cases} \end{equation}
General strategy:
- Find zeros of the right side (which are the stationary solutions)
- Analyze near-stationary solutions through eigenvalues of the linearized Jacobian matrix: if both eigenvalues are zero
- Away from stationary solutions: basically guessing
Three Examples that are Hopeless to Solve
Lotha-Volterra Prey-Predictor Equation
\begin{equation} \begin{cases} x_1’ = 2x_1-x_1x_2 \\ x_2’ = x_1x_2 - 3x_2 \end{cases} \end{equation}
Non-Linear System
Last edited: August 8, 2025“Chaotic Dynamics” Because the word is sadly nonlinear.
motivating non-linearity
\begin{equation} \dv t \mqty(x \\ y) = f\qty(\mqty(x\\y)) \end{equation}
This function is a function from \(f: \mathbb{R}^{2}\to \mathbb{R}^{2}\). All the work on Second-Order Linear Differential Equations, has told us that the above system can serve as a “linearization” of a second order differential equation that looks like the follows:
\begin{equation} \dv t \mqty(x \\y) = A \mqty(x \\ y) +b \end{equation}
non-parametric learning
Last edited: August 8, 2025kernel density estimation
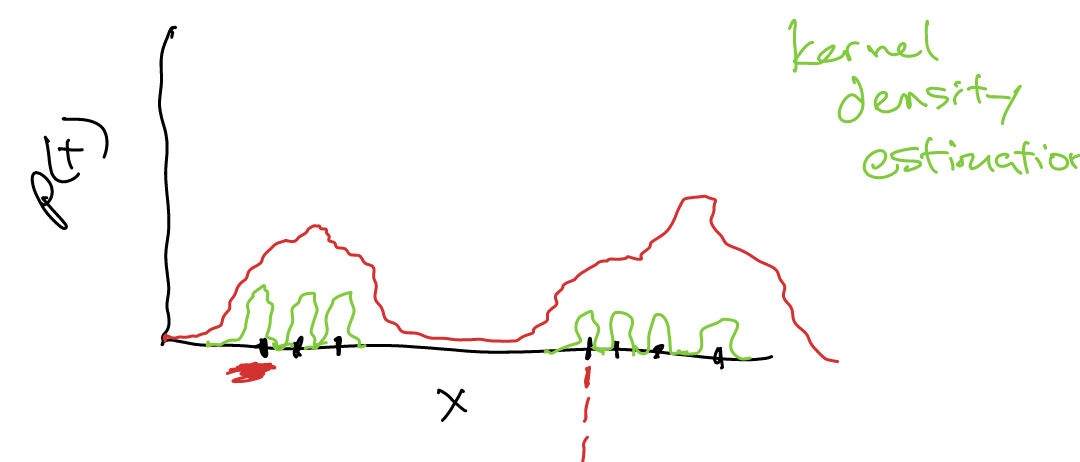
If your data is continuous, you can integrate over the entire dataset and normalize it to be able
non-pathological matricies
Last edited: August 8, 2025Non-Polynomial Time
Last edited: August 8, 2025\begin{equation} NP = \bigcup_{k \in N} \text{NTIME}\qty(n^{k}) \end{equation}
Meaning, these are problems with the property that once you “have” the solution, its “easy” to verify the solution.
verifier formulation of NP
\(L \in \text{NP}\), if there exists a Polynomial Time turing machine named \(V\) (called a “verifier”) such that:
\begin{equation} X \in L \Leftrightarrow \exists\ w \in \qty {0,1}^{\text{poly}\qty(|x|)} V(x,w) = 1 \end{equation}
that is, “yes instances have efficiently checkable certificates/“proofs”
