Define “granularity” as:

\begin{equation} G = \frac{d_{\text{ff}}}{d_{\text{expert}}} \end{equation}

at \(G=1\), we have a dense model; at \(G>1\), we have some kind of MoE.

Here are thy scaling laws:

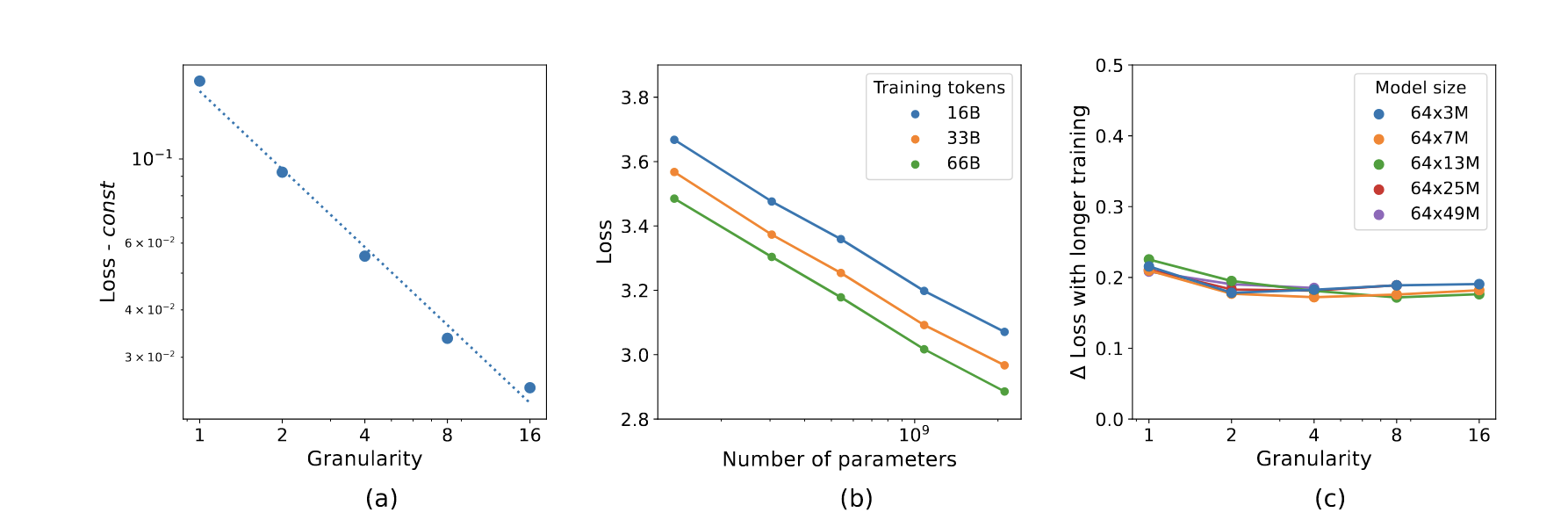
notice how its mostly linear! tiny experts yay!

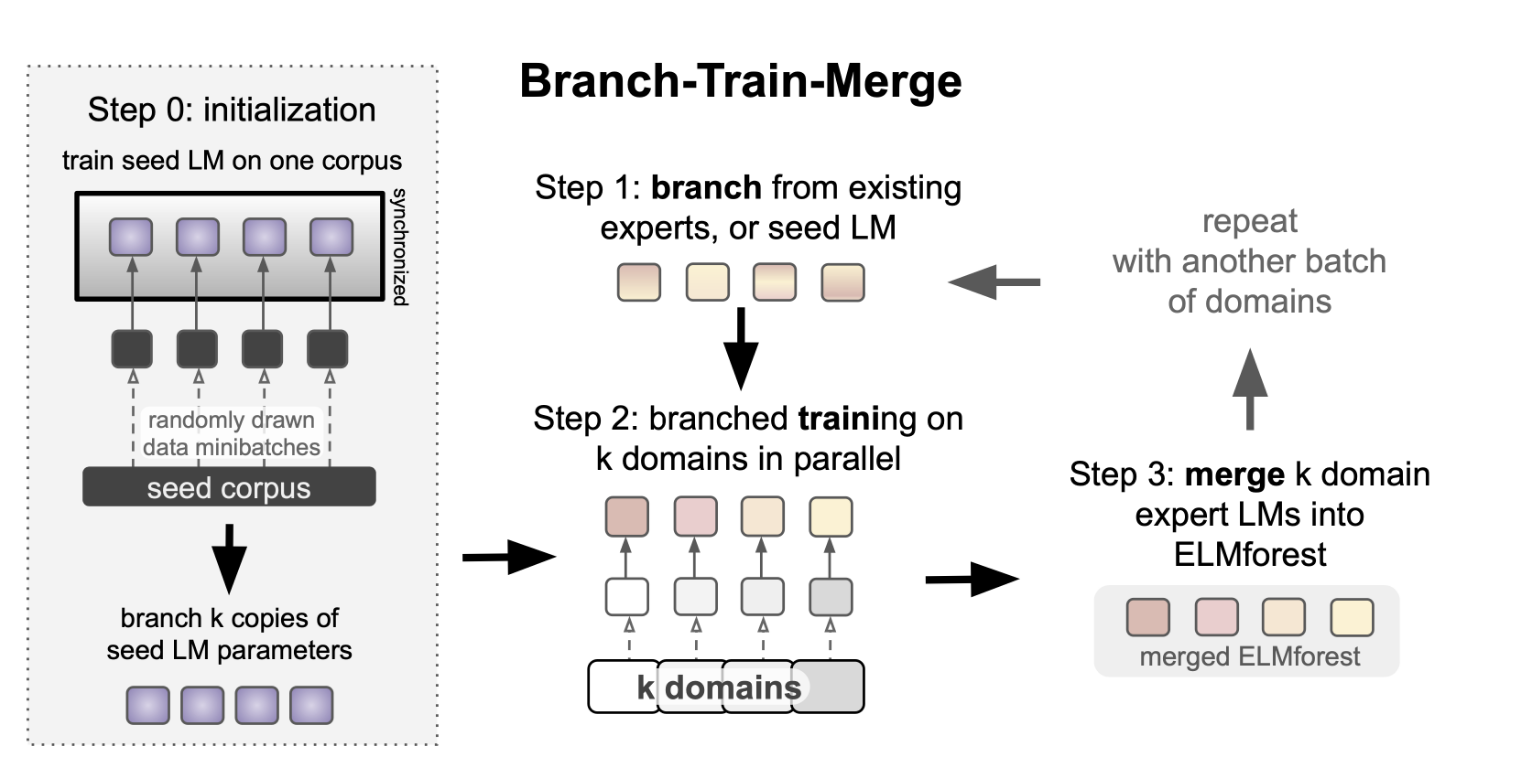
1. weighted parameter average of the existing experts (or copy the new perts)
2. training each expert independently

And then when inference we can use domain-conditioned averaging between the experts by computing:

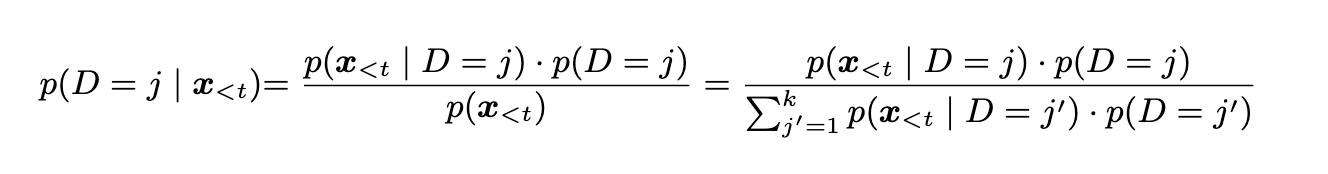
or by averaging the parameters of the experts.

Train experts densely, and then during inference keep only topk

Proposes: more MoEs at later layers + a shared expert.

One-Liner

Getting rid of low singular value components in weights actually improves model performance.

Motivation

Previous work has shown that pruning SVD components works without significant performance degradation. But this work shows that with knowing where to prune more carefully, we can obtain better-than-baseline performance.

Notable Methods

We do this by trying all reductions based on \(\qty(\tau, \ell, \rho)\) tuples where we have \(\tau\) being the parameter type (projs q, k, v, attn out, mlp in and out), \(\ell\) being the layer number, and \(\rho\) being the rate of reduction.