MOEReview Shen: ModuleFormer
Last edited: December 12, 2025The old’ load balancing loss. Instead of training a router with explicitly labeled data for each expert, a load balancing + load concentration loss induces the modularity in data.
Insight: we want to maximize the mutual information between tokens and modules. For the router \(m \sim g\qty(\cdot \mid x)\) (“which module \(m\) should we assign, given token \(x\)”), we write:
\begin{equation} \ell_{MI} = \underbrace{\sum_{m=1}^{N} p\qty(m) \log p\qty(m)}_{-H\qty(m)} - \frac{1}{|X|} \sum_{x \in X}^{} \underbrace{\sum_{m=1}^{N} g\qty(m|x) \log g\qty(m|x)}_{H\qty(m|x)} \end{equation}
MOEReview Sukhbaatar: Branch-Train-MiX
Last edited: December 12, 2025Its MOEReview Li: Branch-Train-Merge but MoEs now. Each layer is combined by standard moe routing with a weight that is tuned.
MOEReview Tan: Scattered MoE
Last edited: December 12, 2025A single kernel to scatter the residuals and then run forward pass at the same time instead of copying and grouping first.
MOEReview Zhang: Mixure of Attention Heads
Last edited: December 12, 2025Split \(Q\) projection and attention out projection into experts, with one router coordinating them.
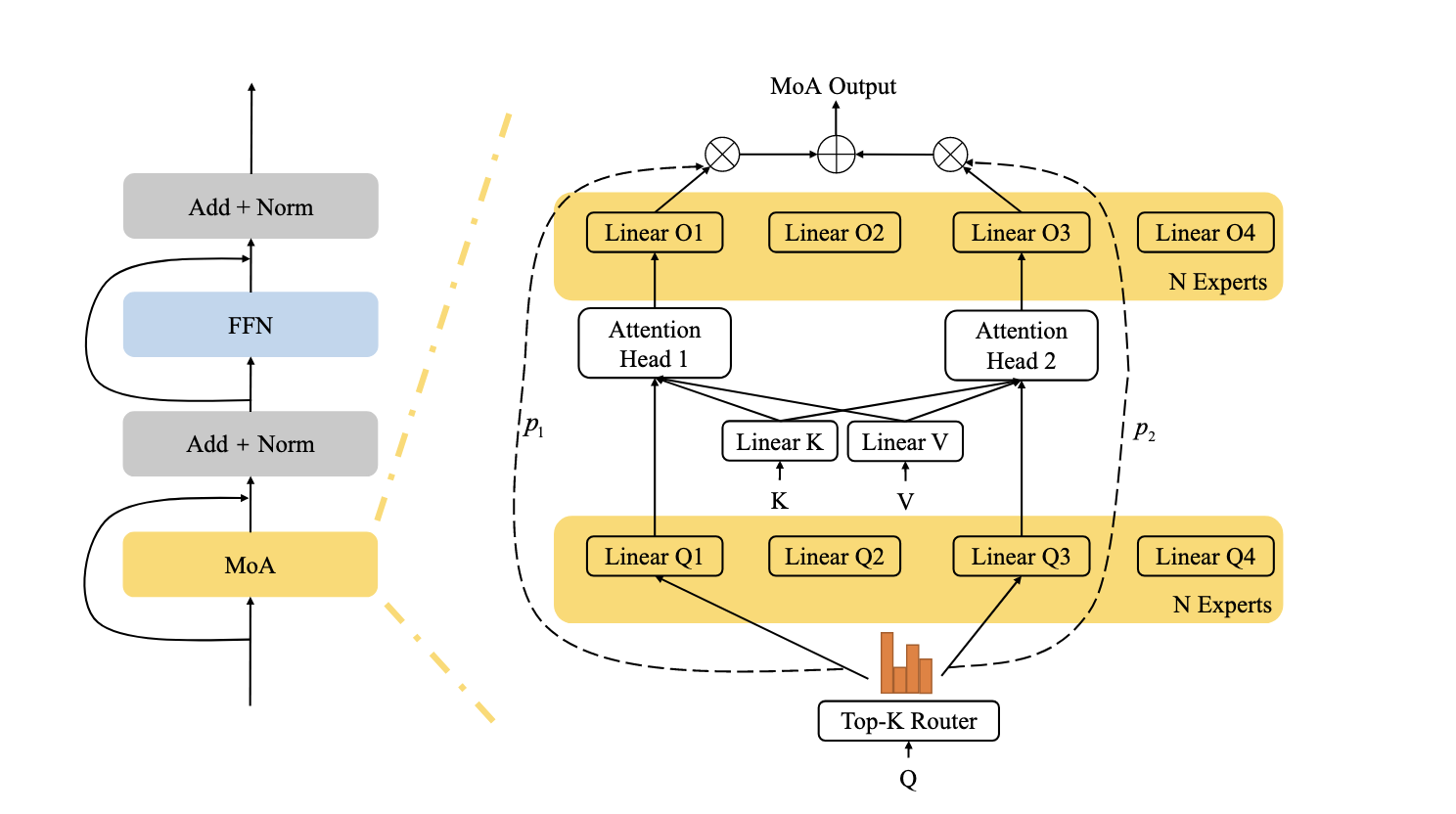
Better than MHA performanec.
Houjun's Academic Home Page
Last edited: December 12, 2025👋 Howdy, I'm Houjun Liu!
I’m a third-year coterminal MSCS and BSCS student in the Computer Science Department at Stanford University, grateful to be advised by Prof. Mykel Kochenderfer. In the course of my research, I have also had the fortunate opportunity to work with Stanford NLP under Prof. Chris Manning, CMU TalkBank under Prof. Brian MacWhinney, and Prof. Xin Liu at UC Davis Engineering. I am affiliated with the Stanford NLP Group and Stanford Intelligent Systems Lab.
