opsin
Last edited: August 8, 2025An opsin is a photo-receptor protein (sensitive to light) that is sensitive to light
Optimal Exploration Policy
Last edited: August 8, 2025Suppose we have offline statistic regarding wins and losses of each slot machine as our state:
\begin{equation} w_1, l_{1}, \dots, w_{n}, l_{n} \end{equation}
What if we want to create a policy that maximises exploration?
We construct a value function:
\begin{equation} U^{*}([w_1, l_{1}, \dots, w_{n}, l_{n}]) = \max_{a} Q^{*}([w_1, l_{1}, \dots, w_{n}, l_{n}], a) \end{equation}
our policy is the greedy policy:
\begin{equation} U^{*}([w_1, l_{1}, \dots, w_{n}, l_{n}]) = \arg\max_{a} Q^{*}([w_1, l_{1}, \dots, w_{n}, l_{n}], a) \end{equation}
Optimal Stopping Problem
Last edited: August 8, 2025- Shuffle cards
- Keep revealing cards
- “Stop” when there’s >50% chance the next card to be revealed is black
We can Frequentist Definition of Probability calculate the probability of a given card remaining is black:
\begin{equation} pblack(b,r) = \frac{26-b}{52-(r+b)} \end{equation}
now:
\begin{equation} pwin(b,r) = \begin{cases} 0, b+r = 52 \\ \max \qty[ \begin{align}&pblack(p,r), \\ &pblack(b,r)pwin(b+1,r) + (1-pblack(b,r)pwin(b, r+1) \end{align}] \end{cases} \end{equation}
“with the theory of the Martingales, this comes out to be 50%”
Optimization Index
Last edited: August 8, 2025AA222/CS361
Applications
Example Objectives
- efficiency
- safety
- accuracy
Example Constraints
- cost
- weight
- (structural) integrity
Why this is hard?
- high dimensional search spaces
- multiple competing objectives
- model uncertainty
Queen Dido’s Problem
- you are granted a plot of land
- how do we surround it with the smallest amount of string?
Design Workflow
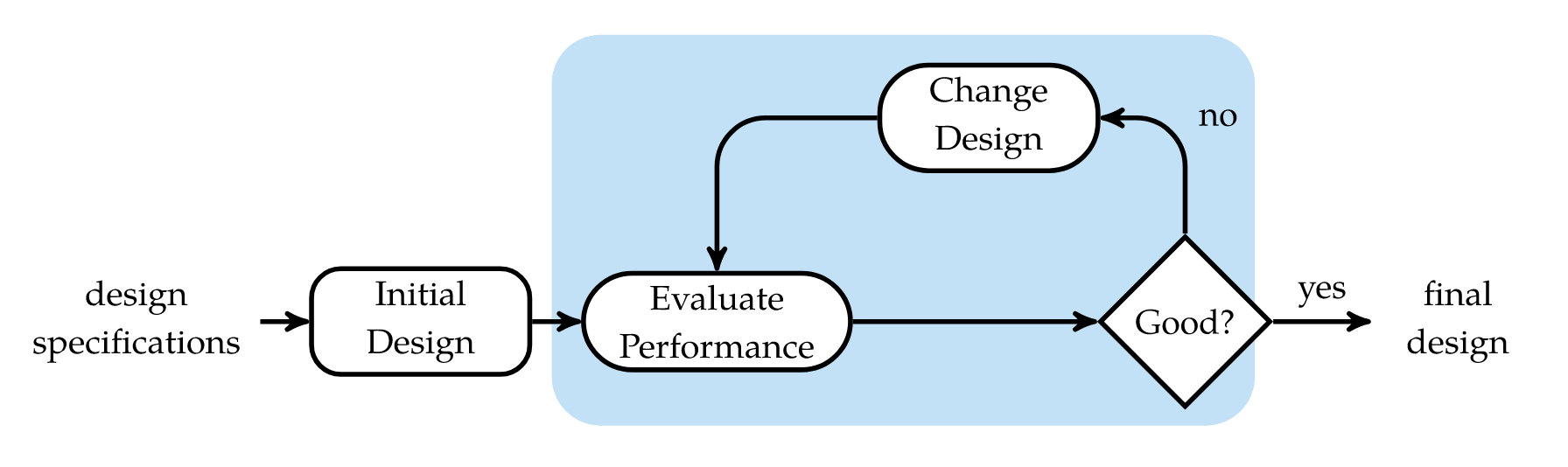
“Optimization: how do we ‘change design’ in response to evaluation”
Logistics
aa222.stanford.edu
Overview
Lectures
Derivatives, Bracketing, Descent, and Approximations
Optimizing Spark
Last edited: August 8, 2025In the event your domain knowledge can help you make decisions about how spark load-balances or stripes data across worker nodes.
Persistence
“you should store this data in faster/slower memory”
MEMORY_ONLY, MEMORY_ONLY_SER, MEMORY_AND_DISK, MEMORY_AND_DISK_SER, DISK_ONLY
rdd.persist(StorageLevel.MEMORY_AND_DISK)
# ... do work ...
rdd.unpersist()
Parallel Programming