\begin{equation} y’ = f(y) \end{equation}

for autonomous ODEs, we can plot a phase line

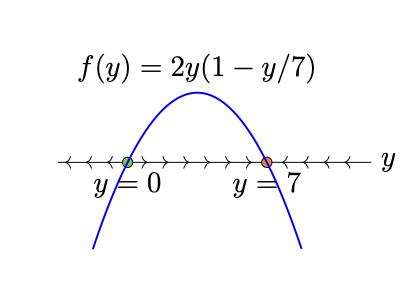
because autonomouse ODEs, we can plot such a line whereby we can analyze the direction of a solution function’s travel

a particle’s one-way motion must converge to a stationary value, or \(\pm \infty\), as \(t\) increases

We will leverage atoms as qubits. So, how do we isolate a qubit from an atom? We will leverage electrons.

We will select the lowest energy state as the base state; as there maybe multiple ground states, we will choose \(|u\big>\) and \(|d\big>\) from two of the states.

physics is the act of explaining what we see in terms of solving for the “unseen”. For an explanation to be good, it needs to be testable.

How exactly does physics work?

“classical results”

• Newton’s laws
• Maxwell’s equations
• General relativity

“quantum theory”

A new model that actually allows particle inference.

(Pineau, Gordon, and Thrun 2006)

PBVI

One-Liner

“If we can avoid the curse of history, the curse of dimensionality wouldn’t be a problem”.

Basically - most POMDP problems don’t reach much of the belief simplex. So, can we concetrate planning on more probable beliefs.

Novelty

1. trajectory based approach to select beliefs
2. belief set is fixed through layers: each backup results in the same number of layers

Notable Methods

PBVI

Key Figs

New Concepts

Notes

pipe chains the STDOUT of one command and put it to the STDIN of another command. Typically, we want to do pipe per direction.

command pipelines

1. span two child processes
2. create a pipe to allow the two processes to communicate
3. connect the first child’s STDOUT to the pipe + the second child’s STDIN to the pipe

pipe()

pipe() gives us back two file descriptors, such that whatever is written to one can be read from another.