MOEReview Sharma: LAZER
Last edited: December 12, 2025One-Liner
Getting rid of low singular value components in weights actually improves model performance.
Motivation
Previous work has shown that pruning SVD components works without significant performance degradation. But this work shows that with knowing where to prune more carefully, we can obtain better-than-baseline performance.
Notable Methods
We do this by trying all reductions based on \(\qty(\tau, \ell, \rho)\) tuples where we have \(\tau\) being the parameter type (projs q, k, v, attn out, mlp in and out), \(\ell\) being the layer number, and \(\rho\) being the rate of reduction.
MOEReview Shen: ModuleFormer
Last edited: December 12, 2025The old’ load balancing loss. Instead of training a router with explicitly labeled data for each expert, a load balancing + load concentration loss induces the modularity in data.
Insight: we want to maximize the mutual information between tokens and modules. For the router \(m \sim g\qty(\cdot \mid x)\) (“which module \(m\) should we assign, given token \(x\)”), we write:
\begin{equation} \ell_{MI} = \underbrace{\sum_{m=1}^{N} p\qty(m) \log p\qty(m)}_{-H\qty(m)} - \frac{1}{|X|} \sum_{x \in X}^{} \underbrace{\sum_{m=1}^{N} g\qty(m|x) \log g\qty(m|x)}_{H\qty(m|x)} \end{equation}
MOEReview Sukhbaatar: Branch-Train-MiX
Last edited: December 12, 2025Its MOEReview Li: Branch-Train-Merge but MoEs now. Each layer is combined by standard moe routing with a weight that is tuned.
MOEReview Tan: Scattered MoE
Last edited: December 12, 2025A single kernel to scatter the residuals and then run forward pass at the same time instead of copying and grouping first.
MOEReview Yun: Inference-Optimal MoEs
Last edited: December 12, 2025“the scaling law (Section 3) shows that more experts (larger E) result in a higher performance; on the other hand, more experts result in a larger inference cost (Section 4.2)”
How do we trade off cost of more experts (in terms of GPU-seconds or dollars, for \(C_0\) being the cost for some per second GPU cost) and performance?
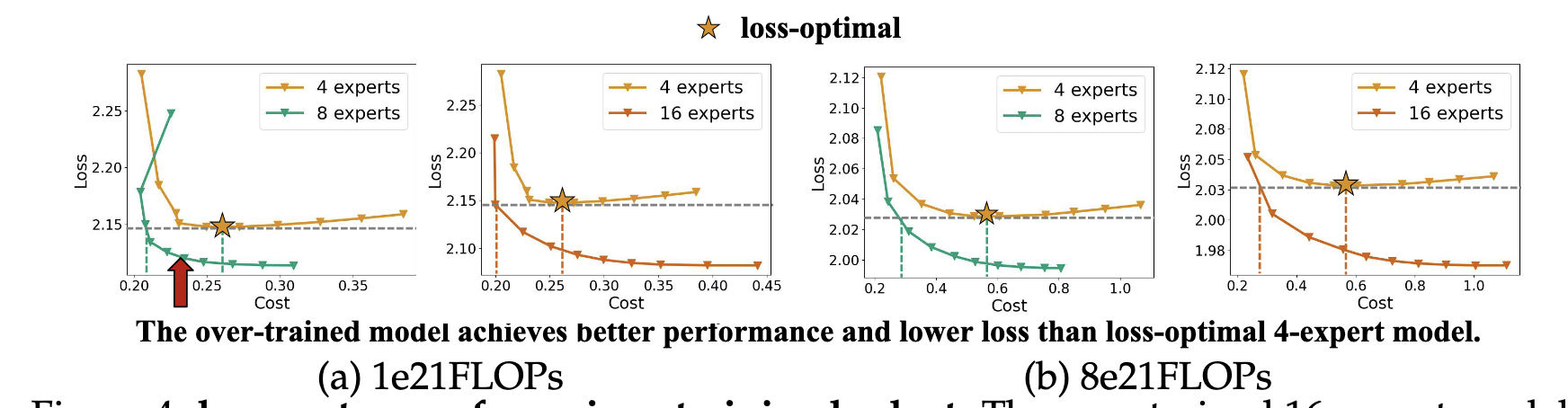
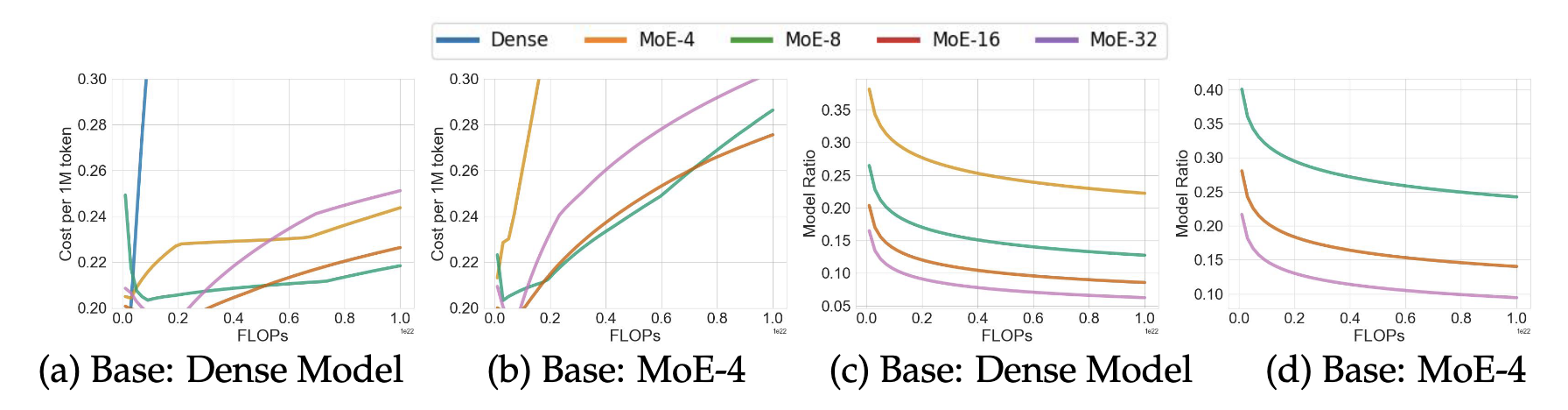
so, slight over-wraiting achieves better performance. Two findings:
- smaller bigger expert (4/8) is the most serving efficient, but costs more to train to the same loss
- with enough data, big (16/32) expert MoE could be smaller, and slight trianing can boost perfromnace
