SU-CS254B APR072025
Last edited: August 8, 2025Recall the relationship between time and space; in particular:
\begin{equation} \text{TIME}\qty(t\qty(n)) \subseteq \text{SPACE}\qty(t\qty(n)) \end{equation}
“space is more valuable than time.”
On time vs. space
\begin{equation} \text{TIME}\qty(\qty(n)) \subseteq \text{SPACE} \qty( \frac{t\qty(n)}{\log \qty(t\qty(n))}) \end{equation}
\begin{equation} \text{TIME}\qty(\qty(n)) \subseteq \text{SPACE}\qty(t\qty(n)) \end{equation}
that is: space is strictly more valuable than time. Oh, and also:
\begin{equation} \text{TIME}\qty(t\qty(n)) \subseteq \text{SPACE}\qty(\sqrt{t\qty(n) \log t\qty(n)}) \end{equation}
Key idea: let’s transform the previous thing into a graph problem!
Suppose \(M\) is the time \(T\) truing machine, and consider its configure at time \(t < T\). Key idea: we can tradeoff time for space! notably, we will solve the same problem using a different algorithm, not modify the original machine.
SU-CS254B APR092025
Last edited: August 8, 2025SU-CS254B APR142025
Last edited: August 8, 2025Some motivations
- time and space are usually considered as independent resources
- but now… consider them as joint (dependent) resources!
question!: what are simultaneous time and space efficient systems? Our interest: time space trade-offs.
Time-Space Tradeoffs
Consider the case that a single TM does something time and space efficiently.
\begin{equation} \text{TISP}\qty(t\qty(n), s \qty(n)) = \qty {L: \exists \text{TM that decides $L$ in time $O(t(n))$, and space $O\qty(s \qty(n))$}} \end{equation}
Some theorems
No algorithm that solves SAT in \(O\qty(n)\) time and \(O\qty(\log n)\) space simultaneously. That is, \(\text{SAT} \not \in \text{TISP}\qty(n, \log n)\).
SU-CS254B APR212025
Last edited: August 8, 2025NP-Intermediate
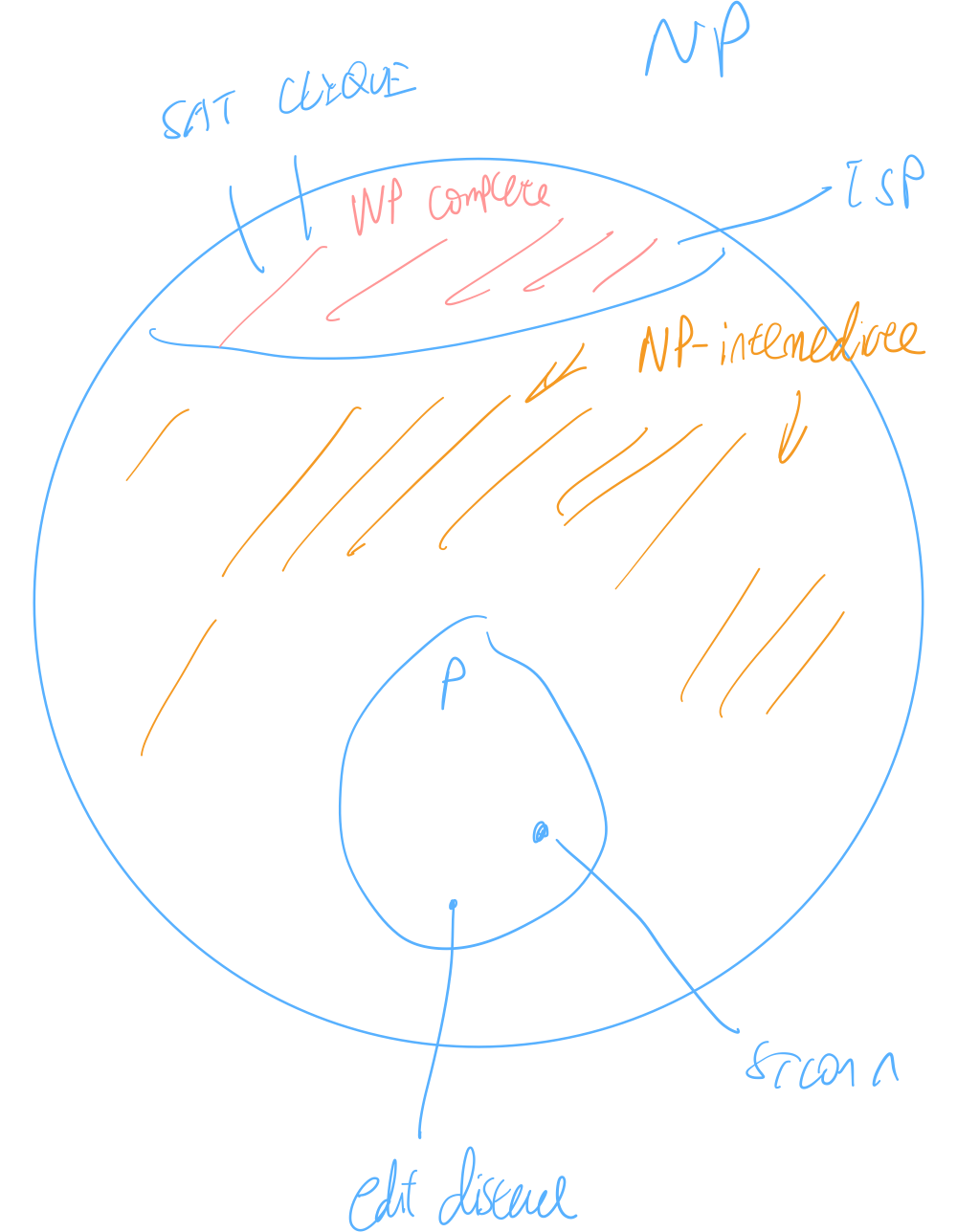
If \(P = NP\), then no distinction between \(P\) and \(NP\), but…
If \(\text{P} \neq \text{NP}\), then exists “NP-intermediate” problem such that \(L \in \text{NP}\) such that \(L \not \in P\) and \(L\) is not NP-complete.
But today, we will prove a weaker’s version.
Ladner’s Theorem
Weaker’s Ladner’s theorem:
Assuming \(\text{SAT}\) requires \(2^{\Omega\qty(n)}\), then there are NP-intermediate languages.
PadSAT
Consider:
\begin{equation} \text{PadSAT}_{m} = \qty {\langle \varphi, 1^{m} \rangle : \varphi \in \text{SAT}} \end{equation}
SU-CS254B APR302025
Last edited: August 8, 2025H*: there’s a language \(A\) such that…
- \(A \in \text{TIME}\qty(2^{O\qty(n)})\)
- \(\exists \delta >0\) such that if \(C_{n}\) is a n-var circuit of size \(\leq 2^{\delta n}\) we have \(\text{Pr}\qty[ C_{n}\qty(x) = A_{n}\qty(x)] \leq \frac{1}{2} + 2^{-\delta n}\)
stretching randomness
Goal: take \(S \sim \qty {\pm 1}^{l}\), we want to stretch this randomness \(\qty {\pm 1}^{n}\) where \(n = 2^{\theta\qty(l)}, l = \theta \qty(\log n)\).
Two main parts:
- combinatorial designs
- Yao’s Next-Bit Prediction Lemma
We can choose sufficiently small \(l\), in particular to be \(l = c \log n\), because then we can iterate over all seeds in time \(2^{l} = n^{c}\).
