sum of subsets
Last edited: August 8, 2025The sum of subsets is the definition of addition upon two subsets.
Apparently, the unions of subsets are almost never subspaces (they don’t produce linearity?) Therefore, we like to work with sum of subsets more.
Remember this has arbitrarily many things!! as a part of the content. When defining, remember to open that possibility.
constituents
Sub-sets of \(V\) named \(U_1, U_2, \dots, U_{m}\)
requirements
The sum of subsets \(U_1, \dots, U_{m}\) is defined as:
\begin{equation} U_1, \dots, U_{m} = \{u_1+\dots+u_{m}: u_1\in U_1, \dots, u_{m} \in U_{m}\} \end{equation}
Sum of Two Dice, Random Variable Edition
Last edited: August 8, 2025Consider “what’s the variable representing the sum of the result of 2 dice?”
\begin{equation} Y = \sum_{i=1}^{2} X \end{equation}
where \(X\) is a random variable representing the result of once dice.
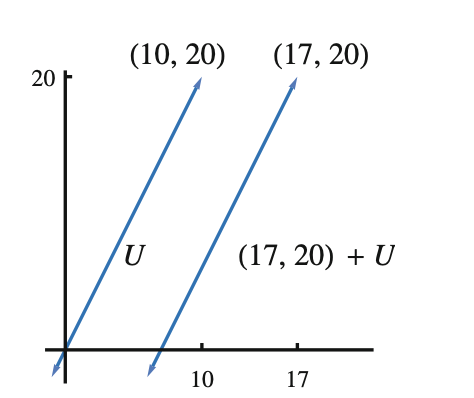
sum of vector and subspace
Last edited: August 8, 2025Suppose \(v \in V\), and \(U \subset V\). Then, \(v+U\) is the subset (not a subspace, obviously):
\begin{equation} v + U = \{v+u : u \in U\} \end{equation}
supersite
Last edited: August 8, 2025supervised learning
Last edited: August 8, 2025Supervised learning (also known as behavioral cloning) if the agent is learning what to do in an observe-act cycle) is a type of decision making method.
constituents
- input space: \(\mathcal{X}\)
- output space: \(\mathcal{Y}\)
- hypothesis/model/prediction: \(h : \mathcal{X} \to \mathcal{Y}\)
requirements
Our ultimate goal is to learn a good model \(h\) from the training set:
- what “good” means is hard to define
- we generally want to use the model on new data, not just the training set
continuous \(\mathcal{Y}\) is then called a regression problem; discrete \(\mathcal{Y}\) is called a classification problem.
