constituents

• \(Q\) is a finite set of states
• \(\Sigma\) is the input alphabet, where \(\square \not \in \Sigma\)
• \(\Gamma\) is the tape alphabet, where \(\square \in \Gamma\), and \(\Sigma \subseteq \Gamma\) (because we can write empty cells)
• \(\delta: Q \times \Gamma \to Q \times \Gamma \times \qty {L, R}\)
• \(q_0 \in Q\), the start state
• \(q_{a} \in Q\), the accept state
• \(q_{r} \neq q_{a}\in Q\), the reject state (because a Turing Machine may not terminate at end of input)

requirements

additional information

why TM is awesome

1. a Turing Machine \(M = \qty(\Gamma, Q, S)\) should be ready for inputs of any length \(n\) (in particular, when designing \(M\), we don’t know what \(n\) will be)
2. a Turing machine’s computation is “local”—you can’t look at the whole input, and the composition of these many local steps
3. No ambiguity as to runtime: how many times you apply \(\delta\) before you get to Qaccept or Qreject

Church-Turing thesis as local steps

“computation is any process that takes place in a sequence of simple, local steps.”

turing machine is a computational system that has a memory tape, and can go through the input multiple times; they don’t have to accept or reject states, turing machines can run forever and can have loops.

For the main topic, see turing machine

decidable vs. recognizable languages

• there are not enough Turing Machines to compute every language (so there are non-recognizable/non-decidable languages)
• halting problem and ATM, meaning strings where Turing Machines can’t decide them
  • “the diagonalization argument”
  • mapping reduction
  • Rice’s Theorem
  • strong reduction: higher achy of hard problems

self-reference

• turing Machines can view and produce its own code.
• foundations of mathematics can be shown using these systems

Kolomogorov Complexity

see Kolomogorov Complexity

\(\text{BPP} \subseteq p / poly\)

Remember the advice-taking TM formulation of circuits.

Now, a language \(L \in \text{BPP}\) if \(\exists\) a polytime TM \(M\) such that:

• \(x \in L\) implies \(P\qty [M\qty(x, v) \text{ accepts}] \geq \frac{2}{3}\)
• \(x \not\in L\) implies \(P\qty [M\qty(x, v) \text{rejects}] \geq \frac{2}{3}\)

Intuition: we want to use \(r\) as advice. But, we need a “random” advice for each \(x\) which we don’t have. But; consider the following parameterization of BPP: we notice that if we have \(\frac{1}{3}\) chance of “bad” advice, we know that we can bump the failure down by trying a more, trending towards \(2^{-O\qty(k)}\). Using \(O\qty(k)\), by the union bound, we know at least one advice is good for all input \(x\).

what if heat, but plate

\begin{equation} \pdv{u}{t} = \pdv[2]{u}{x} + \pdv[2]{u}{y} \end{equation}

For some heat distribution that has arbitrary shape, on some domain \(\Omega \times [0, \infty]_{t}\) (i.e. argumentation of some space dimensions by time).

• Dirichlet Conditions: edges have heat \(0\)
• OR Neumann Conditions: normal derivative (flux) is \(0\) at the edge

If \(\Omega\) is a general blob, you are actually kinda fucked. Because the bounds on \(x\) depend on \(y\), and \(y\) on \(x\), so you can’t just separate them into a product.

Say we want to find the number which is the additive inverse (“negative”) of a number.

We can just flip each of the digit, and then add 1:

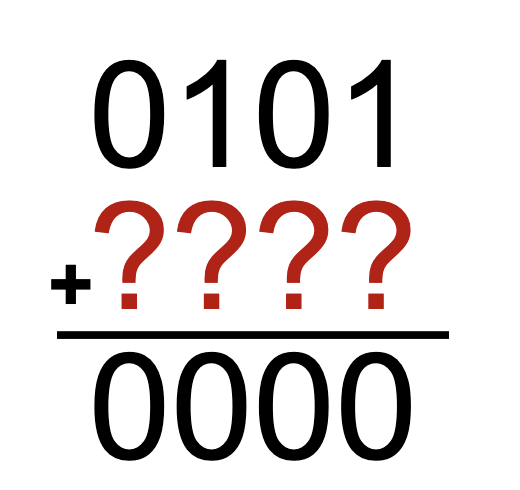
• take \(0101\), invert it to get \(1010\)
• adding these two numbers will give you \(1111\). If we just added one more \(0001\), it will flip over to be \(0000\).
• Therefore, \(1010+0001 = 1011\) is the additive inverse of \(0101\).

The left most bit being one: still a mark of whether or not something is negative. It just works backwards: