unique_lock

Last edited: August 8, 2025

the unique_lock is a mutex management type. Its a lock management system whereby the type will unlock the mutex on your behalf whenever the unique lock goes out of scope.

this is useful if there are multiple paths to exit a function, where an edge case made you forget when to unlock:

void my_scope(mutex &mut, condition_variable_any &cv) {
    unique_lock<mutex> lck(mut);
    // do stuff, you can even pass it to a condition variable!
    cv.wait(lck);
}

Unique-SAT

Last edited: August 8, 2025

Consider UNIQUE-SAT:

for each version of SAT, UNIQUE-SAT has the property that we have either…

no satisfying assignments
exactly one satsifying assignments

We thought that this was esaier than norm SAT, but turns out its exactly as hard.

Valiant-Vazirani

Insights: UNIQUE-SAT isn’t actually easier than SAT (if randomness is allowed). That is:

\begin{equation} \exists \text{rand. poly reduction } \text{SAT} \to \text{UNIQUE-SAT} \end{equation}

Given a n-variable circuit C where our goal is to decide if \(#C \geq 1\) , we can efficiently produce circuits \(C^{(1)},…, C^{(t)}\) such that…

Uniqueness and Existance

Last edited: August 8, 2025

Questions of Uniqueness and Existance are important elements in Differential Equations.

Here’s a very general form of a differential equations. First, here’s the:

function behavior tests

continuity

Weakest statement.

A function is continuous if and only if:

\begin{equation} \lim_{x \to y} f(x) =f(y) \end{equation}

Lipschitz Condition

Stronger statement.

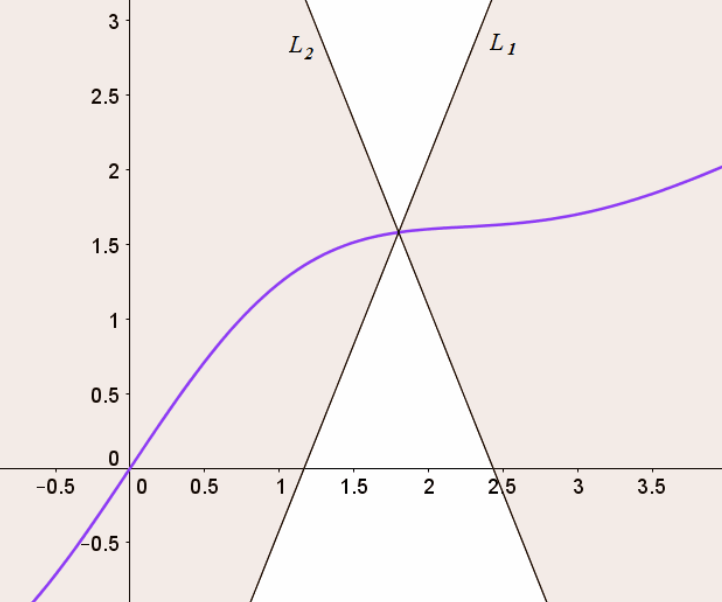
The Lipschitz Condition is a stronger test of Continuity such that:

\begin{equation} || F(t,x)-F(t,y)|| \leq L|| x- y|| \end{equation}

for all \(t \in I\), \(x,y \in \omega\), with \(L \in (0,\infty)\), named “Lipschitz Constant”, in the dependent variable \(x\).

universal quantum constructor

Last edited: August 8, 2025

A constructor built out of quantum theory which can replicate itself. It is considered a universal computer.

universal turing machine

Last edited: August 8, 2025

bit string encoding

encode a finite string in \(\Sigma^{*}\) as a bit string: encoding each character in \(\log | \Sigma |\) bits (by basically IDing each bit).

For \(x \in \Sigma^{*}\), define \(b_{\Sigma}(x)\) to be its binary encoding.

For \(x,y \in \Sigma^{*}\), to encode the pair of strings \(x\) and \(y\), we can encode tuples by adding just a separate symbol \(\Sigma’ = \Sigma \cup \qty {,}\), and then we can write \(x,y\). (if we want to know how long \(x\) is ahead of time we can encode it by show you how long it is through zeros early—\(0^{|b_{\Sigma} (x)|} 1 b_{\Sigma}(x) b_{\Sigma}(y)\).