MOEReview Zhang: Mixure of Attention Heads
Last edited: December 12, 2025Split \(Q\) projection and attention out projection into experts, with one router coordinating them.
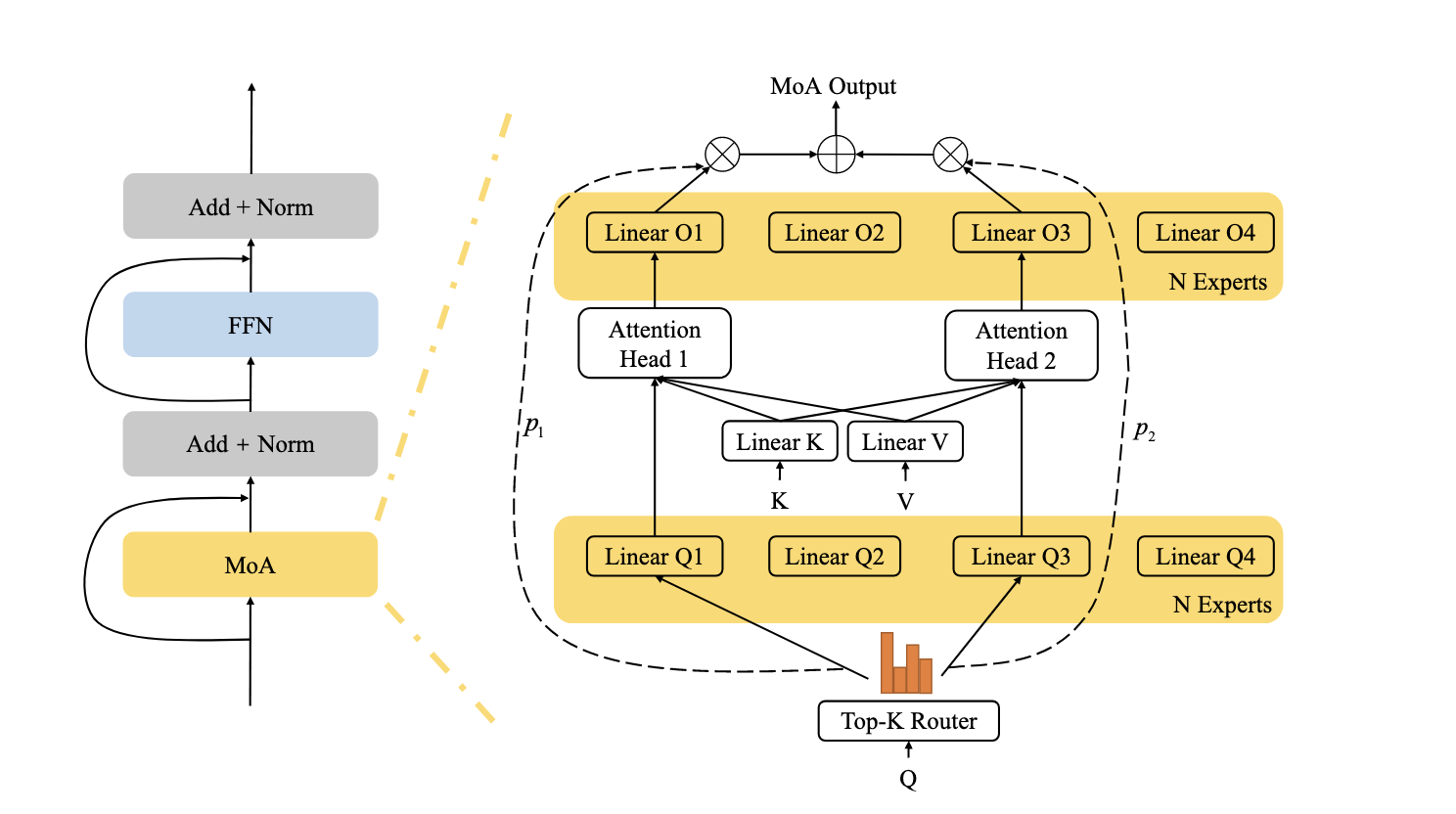
Better than MHA performanec.
Stanford UG Courses Index
Last edited: December 12, 2025Stanford UG Y1, Aut
Stanford UG Y1, Win
Stanford UG Y1, Spr
Stanford UG Y2, Aut
Stanford UG Y2, Win
Stanford UG Y2, Spr
Stanford UG Y3, Aut
Stanford UG Talks
| Date | Topic | Presenter | Link |
|---|---|---|---|
| UG Research Program | Brian Thomas | Stanford UG Research Program | |
| Bld an Ecosystem, Not Monolith | Colin Raffel | Build a System | |
| Training Helpful CHatbots | Nazeen Rajani | Training Helpful Chatbots | |
| AI Intepretability for Bio | Gasper Begus | AI Intepretability | |
| PT Transformers on Long Seqs | Mike Lewis | Pretraining Long Transformers | |
| Transformers! | A. Vaswani | Transformers | |
| Towards Interactive Agents | Jessy Lin | Interactive Agent | |
| Dissociating Language and Thought | Anna Ivanova | Dissociating Language and Thought | |
| Language Agents | Karthik Narasimhan | Language Agents with Karthik | |
| Pretraining Data | |||
| value alignment | Been Kim | LM Alignment | |
| model editing | Peter Hase | Knowledge Editing | |
| Knowledge Localization | |||
| Presentations | Sydney Katz | Presentations | |
| Video Generation with Learned Prior | Meenakshi Sarkar | Priors | |
| Theoretical Drone Control | Sliding Mode UAV Control | ||
| VLM to Agents | Tao Yu | VLM to Agents | |
| Social RL | Natasha Jaques | Social Reinforcement Learning | |
| Model Predictive Control + Prompting | Gabriel Maher | LLM MPC | |
| Planning for Learning | |||
| Theorem Proving | Self-Play Conjection Generalization | ||
| Safety for Trucks | Safety for Autonomous Trucking | ||
| Collaborate Multiagent DM | Collaborative Multiagent DM | ||
| AI Safety Talks | AI Safety Annual Meeting | ||
| Pretraining under infinite compute | Limited Samples and Infinite Compute | ||
| Mel Krusniak | Decisions.jl | ||
| SISL Flash Talks | SISL Talks | ||
| Predicting Scaling Performance | |||
| mixed-autonomy traffic with LLMS | mixed-autonomy traffic with LLMs |
Contacts
Houjun's Academic Home Page
Last edited: December 12, 2025👋 Howdy, I'm Houjun Liu!
I’m a third-year coterminal MSCS and BSCS student in the Computer Science Department at Stanford University, grateful to be advised by Prof. Mykel Kochenderfer. In the course of my research, I have also had the fortunate opportunity to work with Stanford NLP under Prof. Chris Manning, CMU TalkBank under Prof. Brian MacWhinney, and Prof. Xin Liu at UC Davis Engineering. I am affiliated with the Stanford NLP Group and Stanford Intelligent Systems Lab.
Bellman-Ford Algorithm
Last edited: December 12, 2025Bellman-Ford Algorithm is a dynamic programming problem that solves single-source shortest path.
d[v] = \infty
d[s] = 0
for i = 0, ..., n-2:
for v in v:
d_prev = d
for u in v.in_neigbors:
d[v] = min(d_prev[v], d_prev[u] + w(u,v))
Notice you need \(O\qty(n)\) space (2 \(d\) rounds, the previous round and the next round), and runtime is \(O\qty(nm)\) (outer \(n\) loop, inner is an iteration between \(deg\qty(v)*|v| = |e| = m\); that is, we have an minimum over the degree of each \(v\) for every \(v\), which adds up to the total number of edges.)
Dijikstra's Algorithm
Last edited: December 12, 2025constituents
- a weighted directed graph, meaning edges have weights
- where cost of a path is the sum of the weights along that path
- the shortest path is the path with the minimum cost
- starting node \(s\), target node \(t\)
Each node has two states:
- unlabeled
- labeled
And stores a piece of information:
\(d\qty(v) = \text{distance}\qty(s, v)\)
We initialize \(d\qty(v) = \infty, v \neq s\) , and \(d\qty(s) = 0\).
requirements
- pick the node \(u\) that has unlabeled state with smallest \(d\qty(u)\)
- for all neighbor v of u:
- set \(d\qty(v) = \min \qty(d\qty(v), d\qty(u) + \text{edgeWeight}\qty(u,v))\)
- mark \(v\) as labeled
def dike(G,s,t):
set verticies to State.NOTSURE
for v in G.V:
d[v] = float("+inf")
p[v] = None # (for parents)
d[s] = 0
while State.NOTSURE in G.V:
# get node with minimum distance that's not sure
u = argmin(d[v] for v in G.V if v.state == State.NOTSURE)
u.state = State.SURE
for v in u.out_neighbors:
d[v] = min(d[v], d[u] + edgeWeight(u,v))
if d[v] was changed:
p[v] = u # (for obtaining next path in chain for shortes paths)
return d[t]
additional information
proof
Let’s start with a lemma
