atoms as qubits
Last edited: August 8, 2025You can use atoms as many different types of qubits.
manipulating physical qubits
To make physical qubits go to different states, we will again use something in the ancillary states. Rotating it to \(z\) — leverage one lazer to make it fall; \(rx\), \(ry\), we leverage combinations of two light.
various qubit implementations
Implementations of physical qubits
| Type | Superconductor | Ions | Atoms |
|---|---|---|---|
| Company | Google, IBM, Rigetti | IonQ, Honeywell | Atom Computing, QuEra |
| Nature | Artifical | Natural | Natural |
| Calibration | Individual calibration | Naturally calibrated | Naturally calibrated |
| Coherence Time | Short | Long | Long |
| Connectivity | Adjacent connectivity | All-to-all | More than adjacent |
| Scalability | Compatible with existing tech | Not easily scalable | Potentially scalable |
| Speed | Fast gates | Kinda fast | Untested |
possible uses for qubits
Here are some possible uses for physical qubits
Atrial Fibrillation
Last edited: August 8, 2025AFIB is a heart conditinos, which is augmented during heart surgery.
“Endogeneous extrolluculor proteases damage to Kv1.5 in the atria contributes to AFIB”
- WBC’s secretion of proteases, such as calpain when it is inflamed
Authoritarianism
Last edited: August 8, 2025autism
Last edited: August 8, 2025autism is a spectrum disorder that are caused by both environmental and genetic factors.
Key Question: how can different chromatin regulators lead to the same set of symptoms named “autism”.
autism gene signature
The gene signature of autism can be measured in clean and quantitative assays.
Automatic Differentiation
Last edited: August 8, 2025Forward Accumulation
First, make a computation graph.
Consider \(\ln (ab + \max (a,2))\)
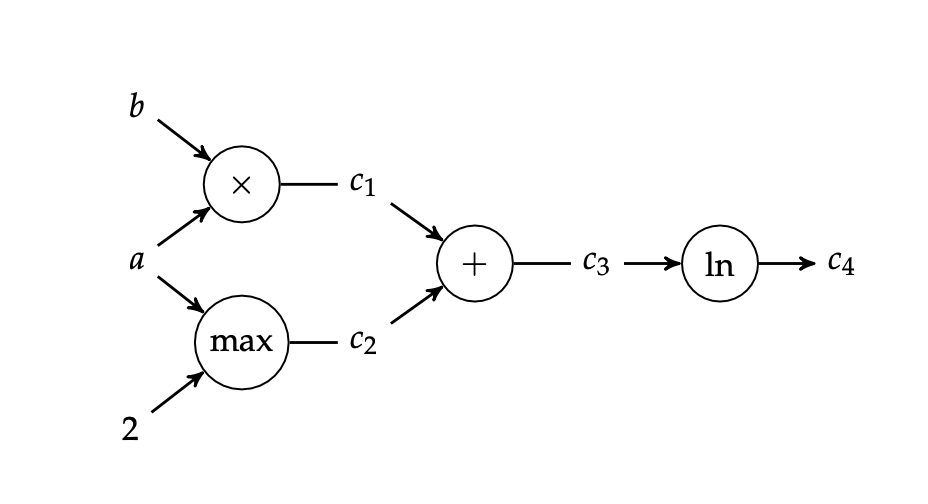
Say we want \(\pdv{f}{a}(3,2)\).
Let’s begin by tracking, left to right, both the value of each node and its derivative.
Layer 1:
- \(b = 2, \pdv{b}{a} = 0\)
- \(a = 3, \pdv{a}{a} = 1\)
Layer 2:
- \(c_1 = a\times b = 6, \pdv{c_1}{a} = b\pdv{a}{a} + a \pdv{a}{b} = 2\)
and so on; until we get to \(c_4\)
