We treat this as an inference problem in Naive Bayes: observations are independent from each other.

Instead of trying to compute a \(\theta\) that works for Maximum Likelihood Parameter Learning, what we instead do is try to understand what \(\theta\) can be in terms of a distribution.

That is, we want to get some:

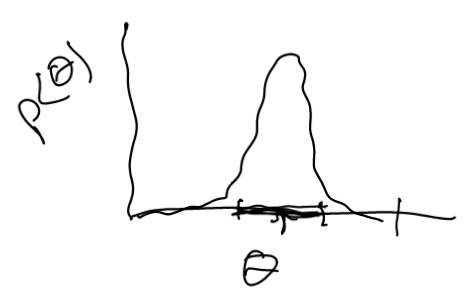
“for each value of \(\theta\), what’s the chance that that is the actual value”

To do this, we desire:

belief is a probability distribution over your states.

“an informational state decoupled from motivational states”

\begin{equation} b \leftarrow update(b,a,o) \end{equation}

There are two main flavours of how to represent beliefs

• parametric: belief distribution is fully represented over all states by a set of parameters (categorical, gaussian, etc.)
• non-parametric: belief is represented by a non-weighted list of possible locations of where you are; such as a Particle Filter

To update parametric beliefs, we can use a discrete state filter (for categorical belief distributions) or a Kalman Filter (for linear Gaussian). To update non-parametric beliefs, we can use a Particle Filter.

Motivation

• Imperfect sensors in robot control: partial observations
• Manipulators face tradeoff between sensing + acting

curse of dimensionality and curse of history.

Belief-Space Planning

Perhaps we should plan over all possible distributions of state space, making a belief-state MDP.

But: this is a nonlinear, stochastic dynamic. In fact: there maybe stochastic events that affects dynamics.

Big problem:

• dim(belief) >> dim(state)
• dim(belief) >> dim(action)

Belief iLQR

“determinize and replan”: simplify the dynamics at each step, plan, take action, and replan

Our belief can be represented as vectors as the probability of us being in each state. If we have that, we can just use our belief vector as our state vector. Now use MDP any solving you’d like, keeping in mind that the reward is just the expected reward:

\begin{equation} \mathbb{E}[R(b,a)] = \sum_{s} R(s,a) b(s) \end{equation}

we can estimate our transition between belief-states like so:

\begin{align} T(b’|b,a) &= P(b’|b,a) \\ &= \sum_{o}^{} P(b’|b,a,o) P(o|b,a) \\ &= \sum_{o}^{} P(b’ = Update(b,a,o)) \sum_{s’}^{}O(o|a,s’) \sum_{s}^{}T(s’|s,a)b(s) \end{align}

Bending is what happens when you apply a transverse load to an object and it goes wooosh.

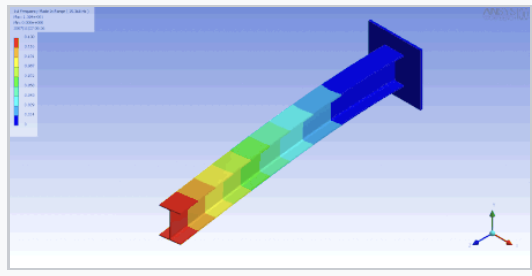
That’s cool. Now how does it work? see Euler-Bernoulli Theory